그리디 알고리즘
★ 그리디 알고리즘
- 최적화 문제를 해결하는 알고리즘
- 욕심쟁이 방법, 탐욕적 방법, 탐욕 알고리즘 등으로 불림
☆ 종류
1. 동전 거스름돈 문제
2. 최소 신장 트리
3. Dijkstra(다익스트라) 최단 경로
4. 부분 배낭 문제
5. 집합 커버 문제
6. 작업 스케줄링 문제
★ 배낭 문제
- 최대의 가치를 갖도록 배낭에 넣을 물건들은 정하는 문제
(-> n개의 물건이 있고, 각 물건은 무게와 가치를 가지고 있으며, 배낭이 한정된 무게의 물건들을 담을 수 있을 경우)
☆ 부분 배낭 (Fractional Knapsack) 문제
- 물건을 부분적으로 담는 것을 허용
- 그리디 알고리즘으로 해결
☆ 0-1 배낭 문제 (0/1 배낭 문제)
- 부분 배낭 문제의 원형으로 물건을 통째로 배낭에 넣어야 함
- 동적 계획 알고리즘, 백트래킹 기법, 분기 한정 기법으로 해결
★ 부분 배낭 문제
- 물건을 부분적으로 배낭에 담을 수 있으므로, 최적해를 위해서 ‘욕심을 내어’ 단위 무게 당 가장 값나가는 물건을 배낭에 넣고, 계속해서 그 다음으로 값나가는 물건을 넣게 됨
- 만일 그 다음으로 값나가는 물건을 ‘통째로’ 배낭에 넣을 수 없게 되면, 배낭에 넣을 수 있을 만큼만 물건을 부분적으로 배낭에 넣음
★ 부분 배낭 문제 그리디 알고리즘
입력: n개의 물건, 각 물건의 무게와 가치, 배낭의 용량 C
출력: 배낭에 담은 물건 리스트 L과 배낭에 담은 물건 가치의 합 v
각 물건에 대해 단위 무게 당 가치를 계산한다.
물건들을 단위 무게 당 가치를 기준으로 내림차순으로 정렬하고, 정렬된 물건 리스트를 S라고 하자.
L=∅, w=0, v=0 // L은 배낭에 담을 물건 리스트, w는 배낭에 담긴 물건들의 무게의 합, v는 배낭에 담긴 물건들의 가치의 합
S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다.
while ( (w+x의 무게) ≤ C ) {
x를 L에 추가시킨다.
w = w+x의 무게
v = v+x의 가치
x를 S에서 제거한다.
S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다. }
if ((C-w) > 0) { // 배낭에 물건을 부분적으로 담을 여유가 있으면
물건 x를 (C-w)만큼만 L에 추가한다.
v = v +(C-w)만큼의 x의 가치 }
return L, v
☆ 알고리즘 수행 과정
- 다음 그림과 같은 4개의 금속 분말이 있고, 배낭의 최대 용량은 40그램이다.




☆ 시간복잡도

☆ 응용
- ‘버리는 부분 최소화시키는’ 원자재 자르기
- 자산투자 및 금융 포트폴리오에서의 최선의 선택
- Merkle–Hellman 배낭 암호 시스템의 키 (Key) 생성
- 0-1 배낭 문제 : 최소의 비용으로 자원을 할당하는 문제로서, 조합론, 계산이론, 암호학, 응용수학 분야에서 기본적인 문제로 다루어짐
★ 집합 커버 문제
- 집합 F에서 선택하는 집합들의 수를 최소화하는 문제
- n개의 원소를 가진 집합 U가 있고, U의 부분집합들을 원소로 하는 집합 F가 주어질 때,
=> F의 원소들인 집합들 중에서 어떤 집합들을 선택하여 합집합하면 U와 같게 되는가?
☆ 예시) 신도시 학교 배치 문제



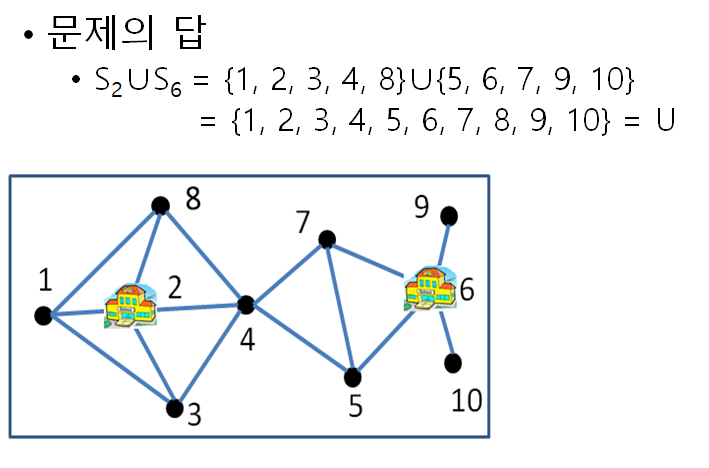
☆ 집합 커버 문제의 최적해

- F에 n개의 원소가 있을 경우 -> 계산시간이 상당히 길어짐
=> 최적해 대신 이에 근접한 근사해(approximation solution)를 찾음
★ 집합 커버 알고리즘


☆ SetCover 알고리즘의 수행 과정





-> SetCover 알고리즘의 최종해는 최적해와 다름!!
☆ 시간복잡도

☆ 응용
- 도시 계획 (City Planning)에서 공공 기관 배치하기
- 경비 시스템: 경비가 요구되는 장소의 CCTV 카메라의 최적 배치
- 컴퓨터 바이러스 찾기
- 대기업의 구매 업체 선정
- 기업의 경력 직원 고용
- 비행기 조종사 스케줄링, 조립 라인 균형화, 정보 검색 등에 활용
★ 작업 스케줄링
- 작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제
- 작업 스케줄링 문제에 주어진 문제 요소
1) 작업의 수
2) 각 작업의 시작시간과 종료시간
3) 작업의 길이 - 작업의 시작시간과 종료시간은 정해져 있으므로 작업의 길이도 주어진 것이다.
- 시작시간, 종료시간, 작업 길이에 대한 그리디 알고리즘
-> 빠른 시작시간 작업 우선 (Earliest start time first) 배정
-> 빠른 종료시간 작업 우선 (Earliest finish time first) 배정
-> 짧은 작업 우선 (Shortest job first) 배정
-> 긴 작업 우선 (Longest job first) 배정
☆ 작업 스케줄링 알고리즘


☆ 알고리즘 수행과정



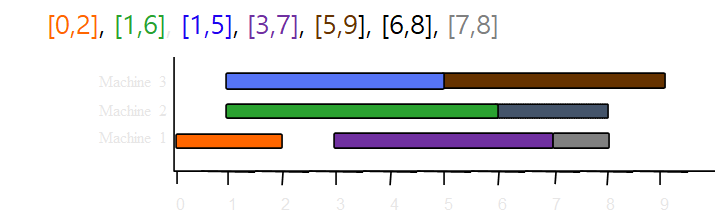
☆ 시간복잡도

☆ 응용
- 비즈니스 프로세싱
- 공장 생산 공정
- 강의실/세미나 룸 배정
- 컴퓨터 태스크 스케줄링 등