이론_전공/알고리즘
Dijkstra(다익스크라)최단경로 알고리즘(그리디 알고리즘)
오뀨기
2020. 11. 1. 21:30
★ 최단 경로(Shortest Path) 문제
- 주어진 가중치 그래프에서 어느 한 출발점에서 또 다른 도착점까지의 최단 경로를 찾는 문제
☆ 최단 경로를 찾는 가장 대표적인 알고리즘
- 다익스트라(Dijkstra) 최단 경로 알고리즘
☆ 다익스트라 알고리즘
- 주어진 출발점에서 시작
- 출발점으로부터 최단 거리가 확정되니 않는 점들 중에서 출발점으로부터 가장 가까운 점을 추가하고, 그 점의 최단 거리를 확정
★ Dijkstra(다익스트라) 알고리즘
ShortestPath(G, s)
입력: 가중치 그래프 G=(V,E), |V|=n , |E|=m
출력: 출발점 s로부터 (n-1)개의 점까지 각각 최단 거리를 저장한 배열 D
1. 배열D를 ∞로 초기화시킨다. 단, D[s]=0으로 초기화한다.
// 배열 D[v]에는 출발점 s로부터 점 v까지의 거리가 저장된다.
2. while(s로부터의 최단거리가 활정되지 않은 점이 있으면){
3. 현재까지 s로부터 최단 거리가 확정되지 않은 각 점 v에 대해서 최소의 D[v]의 값을 가진 점 Vmin을 선택하고,
출발점 s로부터 점 vmin까지의 최단 거리 D[vmin]을 확정한다.
4. s로부터 현재보다 짧은 거리로 점 vmin을 통해 우회 가능한 각 점 w에 대해서 D[w]를 갱신한다. }
5. retun D
★ ShortestPath 알고리즘 수행과정


예시)



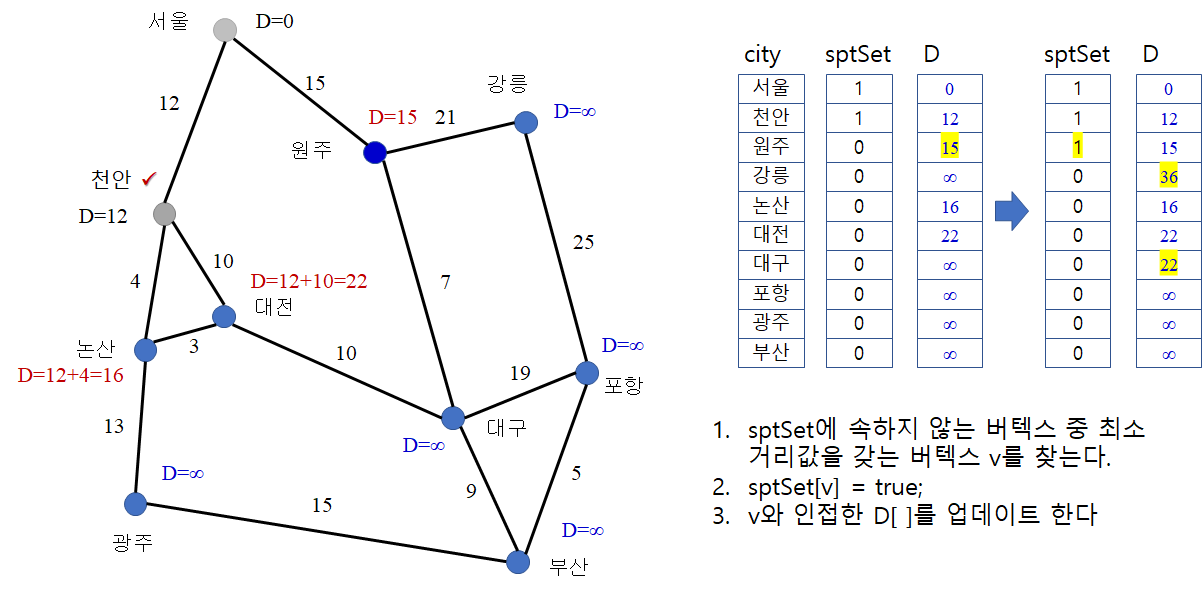






☆ 시간복잡도
- while루프가 (n-1)번 반복되고, 1회 반복될때
: line 3에서 최소의 D[v]를 가진 점 Vmin을 찾는데 O(n) 시간이 걸림(∴ 배열 D에서 최소값을 찾는 것이기 때문)
: line 4에서도 Vmin에 연결된 점의 수가 최대 (n-1)개이므로, 각 D[w]를 갱신하는데 걸리는 시간은 O(n)
-> 시간복잡도 : (n-1)x{O(n)+O(n)} = O(n²)
☆ 응용
- 맵퀘스트(Mapquest)와 구글 (Google) 웹사이트의 지도 서비스
- 자동차 네비게이션
- 네트워크와 통신 분야
- 모바일 네트워크
- 산업 공학과 경영 공학의 운영 (Operation) 연구
- 로봇 공학
- 교통 공학
- VLSI 디자인 분야 등
★ 구현하기
-> 'C# 콘솔 앱'으로 구현!!
-> 코드에 대한 설명은 주석으로 처리함
☆ class 안에 있는 코드
static int V = 10; // 버텍스의 갯수
static string[] city = { "서울", "천안", "원주", "강릉", "논산", "대전", "대구", "포항", "광주", "부산" }; // 도시를 저장할 배열
static bool[] sptSet = new bool[V]; // bool배열 -> 최단경로를 찾으면 'true'로 바꿔주기 위해 사용, shortest path 집합, true이면 포함
static int[] D = new int[V]; // v의 shortest path의 값
☆main코드
static void Main(string[] args)
{
// 2차원 배열로 만든 그래프
int[,] graph = new int[,]
{
{ 0, 12, 15, 0, 0, 0, 0, 0, 0, 0 },
{ 12, 0, 0, 0, 4, 10, 0, 0, 0, 0 },
{ 15, 0, 0, 21, 0, 0, 7, 0, 0, 0 },
{ 0, 0, 21, 0, 0, 0, 0, 25, 0, 0 },
{ 0, 4, 0, 0, 0, 3, 0, 0, 13, 0 },
{ 0, 10, 0, 0, 3, 0, 10, 0, 0, 0 },
{ 0, 0, 7, 0, 0, 10, 0, 19, 0, 9 },
{ 0, 0, 0, 25, 0, 0, 19, 0, 0, 5 },
{ 0, 0, 0, 0, 13, 0, 0, 0, 0, 15 },
{ 0, 0, 0, 0, 0, 0, 9, 5, 15, 0 }
};
ShortestPath(graph, 0); // 0은 처음 시작하는 도시의 인덱스
}
☆ ShortestPath알고리즘
// 본격적인 알고리즘
// graph에 대허서 s 버텍스에서 출발하는 최단경로 구하기
private static void ShortestPath(int[,] graph, int s)
{
// 배열 초기화
for(int i =0;i<V; i++)
{
D[i] = int.MaxValue; // 배열 D에 가장 큰값으로 초기화
sptSet[i] = false; // sptSet 배열은 모두 false로 초기화
}
D[s] = 0; // 첫번째 출발점은 0으로 초기화
//
for(int i =0;i<V-1; i++)
{
int min = MinDistance();
sptSet[min] = true;
// D[]배열을 업데이트 해야함
for(int v=0;v<V;v++)
{
// sptSet배열이 '0'이고 graph에서 i와 v가 연결되어 있고 기존의 D보다 graph가 작을 때
// D[v]의 배열을 D[i] + graph의 값으로 바꿔준다
// 아직 결정되지 않는 버텍스 중에서, min과 연결되었고, 현재까지 알려진 최단경로보다 지금까지 찾아진 경로(min)을 통한 거리가 더 가까우면
if(sptSet[v]==false && graph[min,v] != 0 && D[min] + graph[min,v]<D[v])
{
D[v] = D[min] + graph[i, v];
}
}
//찾아진 경로 출력
Console.WriteLine("최단경로 버텍스 : {0}", city[min]);
// D[]출력함수
PrintDist();
}
}
☆ 도시 출력 함수
private static void PrintDist()
{
for (int i = 0; i < V; i++)
Console.WriteLine("{0} : {1}", city[i], D[i]);
}
☆최솟값찾는 알고리즘
//sptSet[e]에서 '1'이 아닌 것 중에서 D[i]의 값(가중치의 값)이 가장 작은 것을 찾아주는 함수
// 최솟값을 찾는 알고리즘
private static int MinDistance()
{
int min = int.MaxValue;
int minIndex = -1;
for(int i =0; i<V; i++)
{
if(sptSet[i]==false && D[i] <min)
{
min = D[i];
minIndex = i;
}
}
return minIndex;
}
★ 전체 코드
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace A009_Dijkstra
{
class Program
{
static int V = 10; // 버텍스의 갯수
static string[] city = { "서울", "천안", "원주", "강릉", "논산", "대전", "대구", "포항", "광주", "부산" }; // 도시를 저장할 배열
static bool[] sptSet = new bool[V]; // bool배열 -> 최단경로를 찾으면 'true'로 바꿔주기 위해 사용, shortest path 집합, true이면 포함
static int[] D = new int[V]; // v의 shortest path의 값
static void Main(string[] args)
{
// 2차원 배열로 만든 그래프
int[,] graph = new int[,]
{
{ 0, 12, 15, 0, 0, 0, 0, 0, 0, 0 },
{ 12, 0, 0, 0, 4, 10, 0, 0, 0, 0 },
{ 15, 0, 0, 21, 0, 0, 7, 0, 0, 0 },
{ 0, 0, 21, 0, 0, 0, 0, 25, 0, 0 },
{ 0, 4, 0, 0, 0, 3, 0, 0, 13, 0 },
{ 0, 10, 0, 0, 3, 0, 10, 0, 0, 0 },
{ 0, 0, 7, 0, 0, 10, 0, 19, 0, 9 },
{ 0, 0, 0, 25, 0, 0, 19, 0, 0, 5 },
{ 0, 0, 0, 0, 13, 0, 0, 0, 0, 15 },
{ 0, 0, 0, 0, 0, 0, 9, 5, 15, 0 }
};
ShortestPath(graph, 0); // 0은 처음 시작하는 도시의 인덱스
}
// 본격적인 알고리즘
// graph에 대허서 s 버텍스에서 출발하는 최단경로 구하기
private static void ShortestPath(int[,] graph, int s)
{
// 배열 초기화
for(int i =0;i<V; i++)
{
D[i] = int.MaxValue; // 배열 D에 가장 큰값으로 초기화
sptSet[i] = false; // sptSet 배열은 모두 false로 초기화
}
D[s] = 0; // 첫번째 출발점은 0으로 초기화
//
for(int i =0;i<V-1; i++)
{
int min = MinDistance();
sptSet[min] = true;
// D[]배열을 업데이트 해야함
for(int v=0;v<V;v++)
{
// sptSet배열이 '0'이고 graph에서 i와 v가 연결되어 있고 기존의 D보다 graph가 작을 때
// D[v]의 배열을 D[i] + graph의 값으로 바꿔준다
// 아직 결정되지 않는 버텍스 중에서, min과 연결되었고, 현재까지 알려진 최단경로보다 지금까지 찾아진 경로(min)을 통한 거리가 더 가까우면
if(sptSet[v]==false && graph[min,v] != 0 && D[min] + graph[min,v]<D[v])
{
D[v] = D[min] + graph[i, v];
}
}
//찾아진 경로 출력
Console.WriteLine("최단경로 버텍스 : {0}", city[min]);
// D[]출력함수
PrintDist();
}
}
private static void PrintDist()
{
for (int i = 0; i < V; i++)
Console.WriteLine("{0} : {1}", city[i], D[i]);
}
//sptSet[e]에서 '1'이 아닌 것 중에서 D[i]의 값(가중치의 값)이 가장 작은 것을 찾아주는 함수
// 최솟값을 찾는 알고리즘
private static int MinDistance()
{
int min = int.MaxValue;
int minIndex = -1;
for(int i =0; i<V; i++)
{
if(sptSet[i]==false && D[i] <min)
{
min = D[i];
minIndex = i;
}
}
return minIndex;
}
}
}