Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 그리디 알고리즘
- 앱인벤터 구구단
- MySQL 연동
- 앱인벤터 어플만들기
- 분할정복
- 알고리즘 이론
- 앱인벤터 앱만들기
- 분할정복 알고리즘
- C#으로 알고리즘 구현
- 데이터베이스
- TooLLLM_facilitating Large Language Models to Maset 16000+ Real-World APIs
- 오라클로 배우는 데이터베이스 개론과 실습 2판
- timestamp supervision
- 재귀함수
- 앱인벤터 기초
- 이클립스 DB연동
- 수술영상 분류
- 알고리즘
- 수술영상 phase recognition
- LLM 논문
- medical AI
- LLM 논문리뷰
- 알고리즘 공부
- 동적계획 알고리즘
- 앱인벤터 TinyDB
- LaMa2
- c#
- 퀵정렬
- 최소 신장 트리
- 앱인벤터
Archives
- Today
- Total
YJ_Scribbles
#A07_최소 신장 트리(그리디)알고리즘(PRIM) 본문
★ 크러스컬(Kruskal) 알고리즘
- 가중치가 가장 작은 선분이 사이클을 만들지 않을 때에만 ‘욕심내어’ 그 선분을 추가시킨다.
- 가장 작은 엣지부터 사이클이 생기지 않도록 추가해나간다

ㅇ 알고리즘

★ 프림 (Prim) 알고리즘
- 임의의 점 하나를 선택한 후, (n-1)개의 선분을 하나씩 추가시켜 트리를 만든다.
ㅇ수행과정

1) a에서 시작
2) a와 연결된 에지 중 가장 작은 값을 갖는 a-d를 선택
3) Dist[] 배열을 업데이트
4) 다음 작은 값인 a-b를 선택
5) Dist[] 배열을 업데이트(a, b, d가 선택됨)
6) 과정을 버텍스 갯수만큼 반복
-> 선택된 버텍스는 다시 선택되지 않으므로
사이클이 생기지 않는다

ㅇ 알고리즘


★ 프림 (Prim) 알고리즘 코딩하기
1. "콘솔앱(C#)"으로 새 프로젝트 만들기
2. 그래프 그려주는 함수(Graph) 만들기 ("새 파일"로 클래스 만들기)
3. 그래프를 읽어오는 함수(ReadGraph)만들기
4. 그래프 출력하는 함수(PrintGraph)만들기
5. 알고리즘 실행하는 함수(Prim)만들기
6. 텍스트 파일로 그래프 추가하기
namespace A007_Prim
{
class Program
{
static void Main(string[] args)
{
Graph g = new Graph();
g.ReadGraph("graph.txt");
g.PringGraph();
g.Prim(0);
}
}
}( g.(함수이름)으로 만들어 주었기 때문에 모두 클래스 안에 매서드가 생성됨)
using System;
namespace A007_Prim
{
public class Graph
{
internal void ReadGraph(string v)
{
throw new NotImplementedException();
}
internal void PringGraph()
{
throw new NotImplementedException();
}
internal void Prim()
{
throw new NotImplementedException();
}
}
}
ㅇ 텍스트 파일만들기
- 아래를 참고하여 만들기

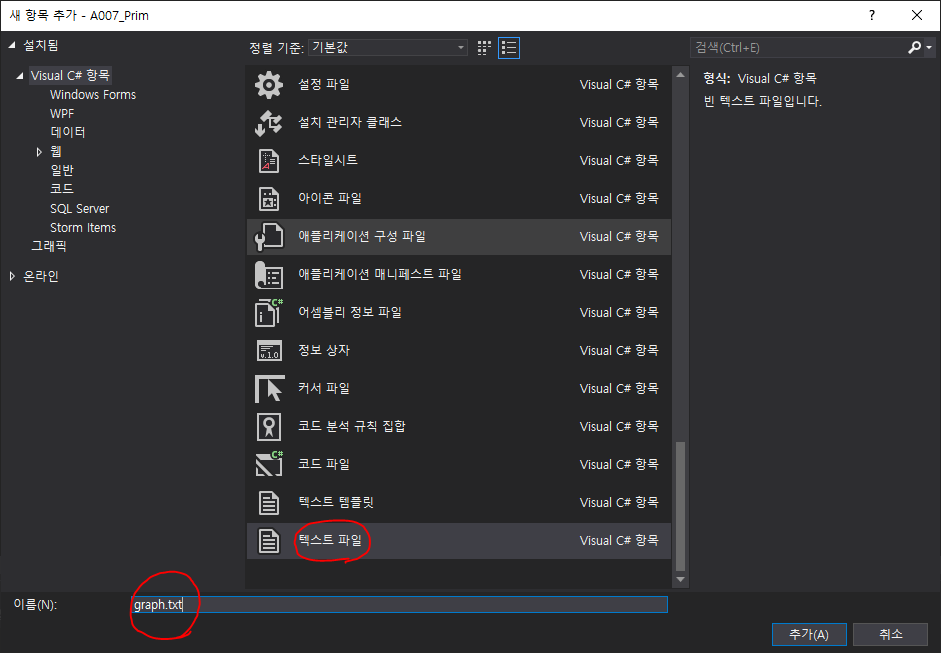

● Graph 클래스 코드 작성하기
ㅇ Graph 안에 다음과 같은 코드 작성
// 데이터 구조 만들기
static int MAX = 100; // 그래프의 최대 버텍스 수
int V = 0; // 현재 그래프에서 버텍스 수
static int INF = 999; // 무한대
// vertex 배열 만들기
string[] vertex = new string[MAX];
//인접배열(2차원)만들기
int[,] adj = new int[MAX, MAX];
ㅇ ReadGraph() 함수 코딩하기
internal void ReadGraph(string fileName)
{
// 파일에서 그래프 가져오기
string[] lines = System.IO.File.ReadAllLines("../../" + fileName);
// vertex의 숫자 처리
V = int.Parse(lines[0]); // 버텍스의 갯수
for(int i = 1;i<lines.Length; i++)
{
// lines[1] : A 0 3 999 2 4 999
string[] split = lines[i].Split('\t');
// vertex[] 배열
vertex[i - 1] = split[0];
for (int j = 1; j < split.Length; j++)
adj[i - 1, j - 1] = int.Parse(split[j]);
}
}
ㅇ PrintGraph() 함수 코딩하기
internal void PringGraph()
{
Console.WriteLine("Vertieces : " + V);
for(int i =0; i<V;i++)
{
Console.Write(vertex[i] + "\t");
for (int j = 0; j < V; j++)
Console.Write("{0,8}", adj[i, j]);
Console.WriteLine();
}
}
ㅇ Prim() 함수 코딩하기
// start 버텍스에서 시작하는 MST를 구하는 과정
public void Prim(int start)
{
// 이미 선택된 버텍스를 저장하는 selected라는 bool 배열
bool[] selected = new bool[MAX];
// 거리를 나타내는 정수배열
int[] dist = new int[MAX];
int MSTWeight = 0;
// 배열 초기화
for(int i =0;i<V;i++)
{
selected[i] = false;
dist[i] = INF;
}
// 시작정점
dist[start] = 0;
for(int i =0;i<V;i++)
{
// 다음번 선택할 가장 작은 값을 갖는 GetMinVertex함수로 가져오기
int u = GetMinVertex(selected, dist);
selected[u] = true;
// 찾아진 값이 무한대일 경우
if (dist[u] == INF)
return;
MSTWeight += dist[u];
// 출력 : 순서랑 거리 모두 나타내기
// Weight의 합 구하기
Console.WriteLine("{0} -> {1} : MST ={2}", vertex[u], dist[u], MSTWeight);
// dist[]을 업데이트(중요)
for(int v =0;v<V;v++)
{
if (adj[u, v] != INF)
if (!selected[v] && adj[u, v] < dist[v])
dist[v] = adj[u, v];
}
}
}
private int GetMinVertex(bool[] selected, int[] dist)
{
int minV = 0; // 최소 정점의 인덱스
int minDist = INF; // 최소 거리
for (int i = 0; i < V; i++)
{
// 선택되지 않은 것들 중에서 찾기
if (!selected[i] && dist[i] < minDist)
{
minV = i;
minDist = dist[i];
}
}
return minV;
}
● 최종 코드
ㅇ 실행 프로그램
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace A007_Prim
{
class Program
{
static void Main(string[] args)
{
Graph g = new Graph();
g.ReadGraph("graph.txt");
g.PringGraph();
g.Prim(0);
}
}
}
ㅇGraph 클래스
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace A007_Prim
{
public class Graph
{
// 데이터 구조 만들기
static int MAX = 100; // 그래프의 최대 버텍스 수
int V = 0; // 현재 그래프에서 버텍스 수
static int INF = 999; // 무한대
// vertex 배열 만들기
string[] vertex = new string[MAX];
//인접배열(2차원)만들기
int[,] adj = new int[MAX, MAX];
internal void ReadGraph(string fileName)
{
// 파일에서 그래프 가져오기
string[] lines = System.IO.File.ReadAllLines("../../" + fileName);
// vertex의 숫자 처리
V = int.Parse(lines[0]); // 버텍스의 갯수
for(int i = 1;i<lines.Length; i++)
{
// lines[1] : A 0 3 999 2 4 999
string[] split = lines[i].Split('\t');
// vertex[] 배열
vertex[i - 1] = split[0];
for (int j = 1; j < split.Length; j++)
adj[i - 1, j - 1] = int.Parse(split[j]);
}
}
internal void PringGraph()
{
Console.WriteLine("Vertieces : " + V);
for(int i =0; i<V;i++)
{
Console.Write(vertex[i] + "\t");
for (int j = 0; j < V; j++)
Console.Write("{0,8}", adj[i, j]);
Console.WriteLine();
}
}
// start 버텍스에서 시작하는 MST를 구하는 과정
public void Prim(int start)
{
// 이미 선택된 버텍스를 저장하는 selected라는 bool 배열
bool[] selected = new bool[MAX];
// 거리를 나타내는 정수배열
int[] dist = new int[MAX];
int MSTWeight = 0;
// 배열 초기화
for(int i =0;i<V;i++)
{
selected[i] = false;
dist[i] = INF;
}
// 시작정점
dist[start] = 0;
for(int i =0;i<V;i++)
{
// 다음번 선택할 가장 작은 값을 갖는 GetMinVertex함수로 가져오기
int u = GetMinVertex(selected, dist);
selected[u] = true;
// 찾아진 값이 무한대일 경우
if (dist[u] == INF)
return;
MSTWeight += dist[u];
// 출력 : 순서랑 거리 모두 나타내기
// Weight의 합 구하기
Console.WriteLine("{0} -> {1} : MST ={2}", vertex[u], dist[u], MSTWeight);
// dist[]을 업데이트(중요)
for(int v =0;v<V;v++)
{
if (adj[u, v] != INF)
if (!selected[v] && adj[u, v] < dist[v])
dist[v] = adj[u, v];
}
}
}
private int GetMinVertex(bool[] selected, int[] dist)
{
int minV = 0; // 최소 정점의 인덱스
int minDist = INF; // 최소 거리
for (int i = 0; i < V; i++)
{
// 선택되지 않은 것들 중에서 찾기
if (!selected[i] && dist[i] < minDist)
{
minV = i;
minDist = dist[i];
}
}
return minV;
}
}
}
★ 실행하기

- 시간복잡도 : O(N²)
★ 예제2
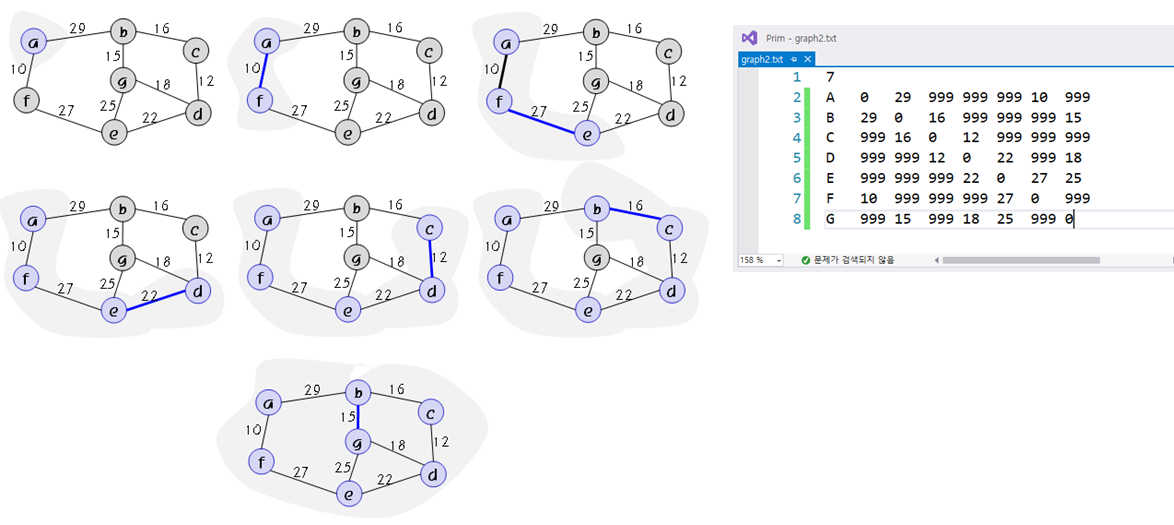
txt 파일을 위의 오른쪽 사진과 같이 추가하여 진행

'이론_전공 > 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘 (0) | 2020.11.09 |
|---|---|
| Dijkstra(다익스크라)최단경로 알고리즘(그리디 알고리즘) (0) | 2020.11.01 |
| 03_그리디알고리즘 (0) | 2020.10.14 |
| #A06_최근접 점의 쌍 분할 정복 알고리즘 (0) | 2020.09.26 |
| 02_이론_분할(Divide)_정복(Conquer)_알고리즘 (0) | 2020.09.26 |




